Введение вспомогательного аргумента в тригонометрических уравнениях. Методы решения тригонометрических уравнений

На уроках алгебры учителя рассказывают, что существует небольшой (на самом деле — очень даже большой) класс тригонометрических уравнений, которые не решаются стандартными способами — ни через разложение на множители, ни через замену переменной, ни даже через однородные слагаемые. В этом случае в дело вступает принципиально другой подход — метод вспомогательного угла.

Что это за метод и как его применять? Для начала вспомним формулы синуса суммы/разности и косинуса суммы/разности:

\[\begin{align}& \sin \left(\alpha \pm \beta \right)=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta \\& \cos \left(\alpha \pm \beta \right)=\cos \alpha \cos \beta \mp \sin \alpha \sin \beta \\\end{align}\]

Думаю, эти формулы хорошо знакомы вам — из них выводятся формулы двойного аргумента, без которых в тригонометрии вообще никуда. Но давайте теперь рассмотрим простое уравнение:

Разделим обе части на 5:

Заметим, что ${{\left(\frac{3}{5} \right)}^{2}}+{{\left(\frac{4}{5} \right)}^{2}}=1$, а это значит, что обязательно найдётся такой угол $\alpha $, для которого эти числа являются соответственно косинусом и синусом. Поэтому наше уравнение перепишется следующим образом:

\[\begin{align}& \cos \alpha \sin x+\sin \alpha \cos x=1 \\& \sin \left(\alpha +x \right)=1 \\\end{align}\]

А это уже легко решается, после чего останется лишь выяснить, чему равен угол $\alpha $. Как это выяснить, а также как правильно подбирать число для деления обеих частей уравнения (в данном простом примере мы делили на 5) — об этом в сегодняшнем видеоуроке:

Сегодня мы будем разбирать решение тригонометрических уравнений, а, точнее, один-единственный прием, который называется «метод вспомогательного угла». Почему именно этот метод? Просто потому, что за последние два-три дня, когда я занимался с учениками, которым рассказывал о решении тригонометрических уравнений, и мы разбирали, в том числе, метод вспомогательного угла, и все ученики как один допускают одну и ту же ошибку. А ведь метод вообщем-то несложный и, более того, это один из основных приемов в тригонометрии. Поэтому многие тригонометрические задачи иначе как методом вспомогательного угла вообще не решаются.

Поэтому сейчас для начала мы рассмотрим пару простеньких задач, а потом перейдем к задачам посерьезней. Однако все эти они так или иначе потребуют от нас применение метода вспомогательного угла, суть которого я расскажу уже в первой конструкции.

Решение простых тригонометрических задач

Пример № 1

\[\cos 2x=\sqrt{3}\sin 2x-1\]

Немного преобразуем наше выражение:

\[\cos 2x-\sqrt{3}\sin 2x=-1\left| \left(-1 \right) \right.\]

\[\sqrt{3}\cdot \sin 2x-\cos 2x=1\]

Как мы будем решать его? Стандартный прием состоит в том, чтобы раскрыть $\sin 2x$ и $\cos 2x$ по формулам двойного угла, а затем переписать единицу как ${{\sin }^{2}}x{{\cos }^{2}}x$, получить однородное уравнение, привести его к тангенсам и решить. Однако это долгий и нудный путь, который требует большого объема вычислений.

Предлагаю задуматься вот на чем. У нас есть $\sin $ и $\cos $. Вспомним формулу косинуса и синуса суммы и разности:

\[\sin \left(\alpha \pm \beta \right)=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta \]

\[\cos \left(\alpha +\beta \right)=\cos \alpha \cos \beta -\sin \alpha \sin \beta \]

\[\cos \left(\alpha -\beta \right)=\cos a\cos \beta +\sin \alpha \sin \beta \]

Вернемся к нашему примеру. Все сведем к синусу разности. Но для начала уравнение необходимо немного преобразовать. Найдем коэффициент:

$\sqrt{l}$ — это тот самый коэффициент, на который необходимо разделить обе части уравнения, чтобы перед синусом и косинусом появились числа, которые сами по себе являются синусами и косинусами. Давайте разделим:

\[\frac{\sqrt{3}}{2}\cdot \sin 2x-\frac{1}{2}\cdot \cos 2x=\frac{1}{2}\]

Посмотрим на то, что у нас получилось слева: существует ли такой $\sin $ и $\cos $, чтобы $\cos \alpha =\frac{\sqrt{3}}{2}$, а $\sin \alpha =\frac{1}{2}$? Очевидно существует: $\alpha =\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$. Поэтому мы можем переписать наше выражение следующим образом:

\[\cos \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\cdot \sin 2x-\sin \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\cdot \cos 2x=\frac{1}{2}\]

\[\sin 2x\cdot \cos \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}-\cos 2x\cdot \sin \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}=\frac{1}{2}\]

Теперь перед нами формула синуса разности. Мы можем написать так:

\[\sin \left(2x-\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}} \right)=\frac{1}{2}\]

Перед нами простейшая классическая тригонометрическая конструкция. Напомню:

Это и запишем для нашего конкретного выражения:

\[\left[ \begin{align}& 2x-\frac{\text{ }\!\!\pi\!\!\text{ }}{6}=\frac{\text{ }\!\!\pi\!\!\text{ }}{6}=2\text{ }\!\!\pi\!\!\text{ }n \\& 2x-\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}=\text{ }\!\!\pi\!\!\text{ }-\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}+2\text{ }\!\!\pi\!\!\text{ }n \\\end{align} \right.\]

\[\left[ \begin{align}& 2x=\frac{\text{ }\!\!\pi\!\!\text{ }}{3}+2\text{ }\!\!\pi\!\!\text{ }n \\& 2x=\text{ }\!\!\pi\!\!\text{ }+2\text{ }\!\!\pi\!\!\text{ }n \\\end{align} \right.\]

\[\left[ \begin{align}& x=\frac{\text{ }\!\!\pi\!\!\text{ }}{6}+\text{ }\!\!\pi\!\!\text{ }n \\& x=\frac{\text{ }\!\!\pi\!\!\text{ }}{2}+\text{ }\!\!\pi\!\!\text{ }n \\\end{align} \right.\]

Нюансы решения

Итак, что нужно делать, если вам попалось подобный пример:

Преобразовать конструкцию, если нужно.
Найти поправочный коэффициент, взять из него корень и разделить обе части примера на него.
Смотрим, какие значения синуса и косинуса получаются у чисел.
Раскладываем уравнение по формулам синуса или косинуса разности или суммы.
Решаем простейшее тригонометрическое уравнение.

В связи с этим у внимательных учеников наверняка возникнет два вопроса.

Что нам мешает на этапе нахождения поправочного коэффициента записать $\sin $ и $\cos $? — Нам мешает основное тригонометрическое тождество. Дело в том, что полученные $\sin $ и $\cos $, как любые другие при одном и том же аргументе, должны при возведении в квадрат в сумме давать ровно «единицу». В процессе решения нужно быть очень внимательным и не потерять «двойку» перед «иксами».

Метод вспомогательного угла — это инструмент, который помогает свести «некрасивое» уравнение к вполне адекватному и «красивому».

Пример № 2

\[\sqrt{3}\sin 2x+2{{\sin }^{2}}x-1=2\cos x\]

Мы видим, что у нас есть ${{\sin }^{2}}x$, поэтому давайте воспользуемся выкладками понижения степеней. Однако прежде чем ними воспользоваться, давайте их выведем. Для этого вспомним, как найти косинус двойного угла:

\[\cos 2x={{\cos }^{2}}x-{{\sin }^{2}}x=2{{\cos }^{2}}x-1=1-2{{\sin }^{2}}x\]

Если мы запишем $\cos 2x$ в третьем варианте, то получим:

\[\cos 2x=1-2{{\sin }^{2}}x\]

\[{{\sin }^{2}}x=\frac{1-{{\cos }^{2}}x}{x}\]

Я выпишу отдельно:

\[{{\sin }^{2}}x=\frac{1-\cos 2x}{2}\]

То же самое можно сделать и для ${{\cos }^{2}}x$:

\[{{\cos }^{2}}x=\frac{1+\cos 2x}{2}\]

Нам потребуется только первые выкладки. Давайте приступим к работе над задачей:

\[\sqrt{3}\cdot \sin 2x+2\cdot \frac{1-\cos 2x}{2}-1=2\cos x\]

\[\sqrt{3}\cdot \sin 2x+1-\cos 2x-1=2\cos x\]

\[\sqrt{3}\cdot \sin 2x-\cos 2x=2\cos x\]

Теперь воспользуемся выкладками косинуса разности. Но для начала посчитаем поправку $l$:

Перепишем с учетом этого факта:

\[\frac{\sqrt{3}}{2}\cdot \sin 2x-\frac{1}{2}\cdot \cos 2x=\cos x\]

В этом случае мы можем записать, что $\frac{\sqrt{3}}{2}=\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$, а $\frac{1}{2}=\cos \frac{\text{ }\!\!\pi\!\!\text{ }}{3}$. Перепишем:

\[\sin \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}\cdot \sin 2x-\cos \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}\cdot \cos 2x=\cos x\]

\[-\cos \left(\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}+2x \right)=\cos x\]

Внесем «минус» в скобку хитрым способом. Для этого заметим следующее:

\[\cos \left(\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}+2x \right)=\cos \left(\text{ }\!\!\pi\!\!\text{ }-\text{ }\!\!\pi\!\!\text{ +}\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}+2x \right)=\]

\[=\cos \left(\text{ }\!\!\pi\!\!\text{ }-\frac{2\text{ }\!\!\pi\!\!\text{ }}{3}+2x \right)=\cos \left(\text{ }\!\!\pi\!\!\text{ }+\varphi \right)=-\cos \varphi \]

Возвращаемся к нашему выражению и вспоминаем, что в роли $\varphi $ у нас выражение $-\frac{2\text{ }\!\!\pi\!\!\text{ }}{3}+2x$. Поэтому запишем:

\[-\left(-\cos \left(-\frac{2\text{ }\!\!\pi\!\!\text{ }}{3}+2x \right) \right)=\cos x\]

\[\cos \left(2x-\frac{2\text{ }\!\!\pi\!\!\text{ }}{3} \right)=\cos x\]

Чтобы решить подобною задачу, нужно вспомнить такое:

\[\cos \alpha =\cos \beta \]

\[\left[ \begin{align}& \alpha =\beta +2\text{ }\!\!\pi\!\!\text{ }n \\& \alpha =-\beta +2\text{ }\!\!\pi\!\!\text{ }n \\\end{align} \right.\]

Разберемся с нашим примером:

\[\left[ \begin{align}& 2x-\frac{2\text{ }\!\!\pi\!\!\text{ }}{3}=x+2\text{ }\!\!\pi\!\!\text{ }n \\& 2x-\frac{2\text{ }\!\!\pi\!\!\text{ }}{3}=-x+2\text{ }\!\!\pi\!\!\text{ }n \\\end{align} \right.\]

Давайте посчитаем каждое из этих уравнений:

И вторую:

Запишем окончательный ответ:

\[\left[ \begin{align}& x=\frac{2\text{ }\!\!\pi\!\!\text{ }}{3}+2\text{ }\!\!\pi\!\!\text{ }n \\& x=\frac{2\text{ }\!\!\pi\!\!\text{ }}{9}+\frac{2\text{ }\!\!\pi\!\!\text{ }n}{3} \\\end{align} \right.\]

Нюансы решения

На самом деле, это выражение решается множеством различных способов, однако именно метод вспомогательного угла является в данном случае оптимальным. Кроме того, на примере данной конструкции хотелось бы обратить ваше внимание еще на несколько интересных приемов и фактов:

Формулы понижения степеней. Эти формулы не нужно запоминать, однако нужно знать, как их выводить, о чем я вам сегодня и рассказал.
Решение уравнений вида $\cos \alpha =\cos \beta $.
Добавление «нуля».

Но и это еще не все. До сих пор $\sin $ и $\cos $, которые мы выводили в качестве дополнительного аргумента, мы считали, что они должны быть положительными. Поэтому сейчас мы решим более сложные задачи.

Разбор более сложных задач

Пример № 1

\[\sin 3x+4{{\sin }^{3}}x+4\cos x=5\]

Преобразуем первое слагаемое:

\[\sin 3x=\sin \left(2x+x \right)=\sin 2x\cdot \cos x+\cos 2x\cdot \sin x\]

\[=2\left(1-\cos 2x \right)\cdot \sin x\]

А теперь подставим все это в нашу исходную конструкцию:

\[\sin 2x\cos x+\cos 2x\sin x+2\sin x-2\cos x\sin x+4\cos x=5\]

\[\sin 2x\cos x-\operatorname{cosx}-cos2\sin x+2\sin x+4\cos x=5\]

\[\sin \left(2x-x \right)+2\sin x+4\cos x=5\]

Давайте введем нашу поправку:

Записываем:

\[\frac{3}{5}\sin x+\frac{4}{5}\cos x=1\]

Таких $\alpha $, для которых $\sin $ или $\cos $ был бы равен $\frac{3}{5}$ и $\frac{4}{5}$ в тригонометрической таблице нет. Поэтому давайте просто так и напишем и сведем выражение к синусу суммы:

\[\sin x\cdot \cos \varphi +\cos x\cdot \sin \varphi =1\]

\[\sin \left(x+\varphi \right)=1\]

Это частный случай, простейшая тригонометрическая конструкция:

Осталось найти, чему равен $\varphi $. Именно в этом месте многие ученики ошибаются. Дело в том, что на $\varphi $ накладываются два требования:

\[\left\{ \begin{align}& \cos \varphi =\frac{3}{5} \\& \sin \varphi =\frac{4}{5} \\\end{align} \right.\]

Начертим радар и посмотрим, где такие значения встречаются:

Возвращаясь к нашему выражению, мы напишем следующее:

Но и эту запись можно немного оптимизировать. Поскольку мы знаем следующее:

\[\alpha:\arcsin \alpha +\arccos \alpha =\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}},\]

то в нашем случае можно записать так:

Пример № 2

Здесь потребуется еще более глубокое понимание методик решения стандартных задач без тригонометрии. Но для решения этого примера мы также используем метод вспомогательного угла.\[\]

Первое, что бросается в глаза — здесь нет степеней выше первой и поэтому ничего нельзя разложить по формулам разложения степеней. Воспользуется обратными выкладками:

Зачем я разложил $5$. Вот смотрите:

Единицу по основному тригонометрическому тождеству мы можем расписать как ${{\sin }^{2}}x+{{\cos }^{2}}x$:

Что дает нам такая запись? Дело в том, что в первой скобке стоит точный квадрат. Свернем его и получим:

Предлагаю ввести новую переменную:

\[\sin x+\cos x=t\]

В этом случае мы получим выражение:

\[{{t}_{1}}=\frac{5+1}{4}=\frac{3}{2}\]

\[{{t}_{2}}=\frac{5-1}{4}=1\]

Итого мы получаем:

\[\left[ \begin{align}& \sin x+\cos x=\frac{3}{2} \\& \sin x+\cos x=1 \\\end{align} \right.\]

Разумеется, знающие ученики сейчас скажут, что такие конструкции легко решаются с помощью сведения к однородному. Однако мы решим каждое уравнение методом вспомогательного угла. Для этого сначала посчитаем поправку $l$:

\[\sqrt{l}=\sqrt{2}\]

Разделим все на $\sqrt{2}$:

\[\left[ \begin{align}& \frac{\sqrt{2}}{2}\sin x+\frac{\sqrt{2}}{2}\cos x=\frac{3}{2\sqrt{2}} \\& \frac{\sqrt{2}}{2}\sin x+\frac{\sqrt{2}}{2}\cos x=\frac{\sqrt{2}}{2} \\\end{align} \right.\]

Все сведем к $\cos $:

\[\cos x\cdot \cos \frac{\text{ }\!\!\pi\!\!\text{ }}{4}+\sin x\sin \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\]

\[\left[ \begin{align}& \cos \left(x-\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}} \right)=\frac{3}{2\sqrt{2}} \\& \cos \left(x-\frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)=\frac{\sqrt{2}}{2} \\\end{align} \right.\]

Разбираемся с каждым из этих выражений.

Первое уравнение корней не имеет, и для доказательства этого факта нам поможет иррациональность в знаменателе. Заметим следующее:

\[\sqrt{2}<1,5\]

\[\frac{3}{2\sqrt{2}}>\frac{3}{3\cdot 1,5}=\frac{3}{3}=1\]

Итого мы четко доказали, что требуется, чтобы $\cos \left(x-\frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)$ был равен числу, которое большее «единицы» и, следовательно, у этой конструкции корней нет.

Разбираемся со вторым:

Решаем эту конструкцию:

В принципе, можно оставить ответ таким, а можно его расписать:

Важные моменты

В заключение хотел бы еще раз обратить ваше внимание на работу с «некрасивыми» аргументами, т.е. когда $\sin $ и $\cos $ не являются табличными значениями. Проблема состоит в том, что если мы утверждаем, что в нашем уравнении $\frac{3}{5}$ — это $\cos $, а $\frac{4}{5}$ — это $\sin $, то в итоге, после того как мы решим конструкцию, нужно учитывать оба этих требования. Мы получаем систему из двух уравнений. Если мы не будем это учитывать, то получим следующую ситуацию. В этом случае мы получим две точки и на месте $\varphi $ у нас окажется два числа: $\arcsin \frac{4}{5}$ и $-\arcsin \frac{4}{5}$, однако последний нас ни в коем случае не устраивает. То же самое будет и с точкой $\frac{3}{5}$.

Такая проблема возникает только тогда, когда речь идет о «некрасивых» аргументах. Когда у нас табличные значения, то ничего такого нет.

Надеюсь, сегодняшний урок помог вам разобраться, что такое метод вспомогательного угла и как его применять на примерах разного уровня сложности. Но это не единственный урок, посвященный решению задач методом вспомогательного угла. Поэтому оставайтесь с нами!

Методы решения тригонометрических уравнений.

Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнения для получения его простейшего вида (см. выше ) и решение полученного простейшего тригонометрического уравнения. Существует семь основных методов решения тригонометрических уравнений.

1. Алгебраический метод.

(метод замены переменной и подстановки).

2. Разложение на множители.

П р и м е р 1. Решить уравнение: sin x + cos x = 1 .

Р е ш е н и е. Перенесём все члены уравнения влево:

Sin x + cos x – 1 = 0 ,

Преобразуем и разложим на множители выражение в

Левой части уравнения:

П р и м е р 2. Решить уравнение: cos 2 x + sin x · cos x = 1.

Р е ш е н и е. cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0 ,

Sin x · cos x – sin 2 x = 0 ,

Sin x · (cos x – sin x ) = 0 ,

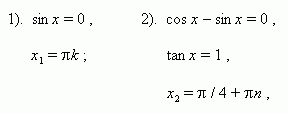
П р и м е р 3. Решить уравнение: cos 2 x – cos 8 x + cos 6 x = 1.

Р е ш е н и е. cos 2 x + cos 6 x = 1 + cos 8 x ,

2 cos 4x cos 2x = 2 cos ² 4x ,

Cos 4x · (cos 2x – cos 4x ) = 0 ,

Cos 4x · 2 sin 3x · sin x = 0 ,

1). cos 4x = 0 , 2). sin 3x = 0 , 3). sin x = 0 ,

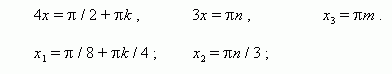
3. Приведение к однородному уравнению.

Уравнение называется однородным от носительно sin и cos , если все его члены одной и той же степени относительно sin и cos одного и того же угла . Чтобы решить однородное уравнение, надо:

а ) перенести все его члены в левую часть;

б ) вынести все общие множители за скобки;

в ) приравнять все множители и скобки нулю;

г ) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на

cos (или sin ) в старшей степени;

д ) решить полученное алгебраическое уравнение относительно tan .

sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2.

Р е ш е н и е. 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x ,

Sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0 ,

Tan 2 x + 4 tan x + 3 = 0 , отсюда y 2 + 4y +3 = 0 ,

Корни этого уравнения: y 1 = - 1, y 2 = - 3, отсюда

1) tan x = –1, 2) tan x = –3,

4. Переход к половинному углу.

Рассмотрим этот метод на примере:

П р и м е р. Решить уравнение: 3 sin x – 5 cos x = 7.

Р е ш е н и е. 6 sin (x / 2) · cos (x / 2) – 5 cos ² (x / 2) + 5 sin ² (x / 2) =

7 sin ² (x / 2) + 7 cos ² (x / 2) ,

2 sin ² (x / 2) – 6 sin (x / 2) · cos (x / 2) + 12 cos ² (x / 2) = 0 ,

tan ² (x / 2) – 3 tan (x / 2) + 6 = 0 ,

. . . . . . . . . .

5. Введение вспомогательного угла.

Рассмотрим уравнение вида :

a sin x + b cos x = c ,

Где a , b , c – коэффициенты; x – неизвестное.

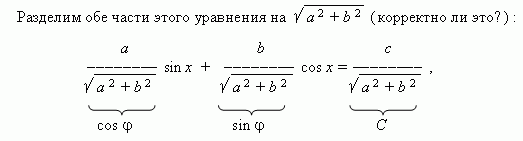
Теперь коэффициенты уравнения обладают свойствами синуса и косинуса , а именно : модуль ( абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1 . Тогда можно обозначить их соответственно как cos и sin (здесь - так называемый вспомогательный угол ), и наше уравнение прини

Элементарные тригонометрические уравнения --- это уравнения вида, где --- одна из тригонометрических функций: , .

Элементарные тригонометрические уравнения имеют бесконечно много корней. Например, уравнению удовлетворяют следующие значения: , и т. д. Общая формула по которой находятся все корни уравнения, где, такова:

Здесь может принимать любые целые значения, каждому из них соответствует определенный корень уравнения; в этой формуле (равно как и в других формулах, по которым решаются элементарные тригонометрические уравнения) называют параметром . Записывают обычно, подчеркивая тем самым, что параметр принимать любые целые значения.

Решения уравнения, где, находятся по формуле

Уравнение решается применяя формулу

а уравнение --- по формуле

Особо отметим некоторые частные случаи элементраных тригонометрических уравнений, когда решение может быть записано без применения общих формул:

При решении тригонометрических уравнений важную роль играет период тригонометрических функций. Поэтому приведем две полезные теоремы:

Теорема Если --- основной период функции, то число является основным периодом функции.

Периоды функций и называются соизмеримыми, если существуют натуральные числа и, что.

Теорема Если периодические функции и, имеют соизмеримые и, то они имеют общий период, который является периодом функций, .

В теореме говорится о том, что является периодом функции, и не обязательно является основным периодом. Например, основной период функций и --- , а основной период их произведения --- .

Введение вспомогательного аргумента

Стандартным путем преобразования выражений вида является следующий прием: пусть --- угол, задаваемый равенствами, . Для любых и такой угол существует. Таким образом. Если, или, в других случаях.

Схема решения тригонометрических уравнений

Основная схема, которой мы будем руководствоваться при решении тригонометрических уравнений следующая:

решение заданного уравнения сводится к решению элементарных уравнений. Средства решения --- преобразования, разложения на множители, замена неизвестных. Ведущий принцип --- не терять корней. Это означает, что при переходе к следующему уравнению (уравнениям) мы не опасаемся появления лишних (посторонних) корней, а заботимся лишь о том, чтобы каждое последующее уравнение нашей "цепочки" (или совокупность уравнений в случае ветвления) являлось следствием предыдущего. Одним из возможных методов отбора корней является проверка. Сразу заметим, что в случае тригонометрических уравнений трудности, связанные с отбором корней, с проверкой, как правило, резко возрастают по сравнению с алгебраическими уравнениями. Ведь проверять приходится серии, состоящие из бесконечного числа членов.

Особо следует сказать о замене неизвестных при решении тригонометрических уравнений. В большинстве случаев после нужной замены получается алгебраическое уравнение. Более того, не так уж и редки уравнения, которые, хотя и являются тригонометрическими по внешнему виду, по существу таковыми не являются, поскольку уже после первого шага --- замены переменных --- превращаются в алгебраические, а возращение к тригонометрии происходит лишь на этапе решения элементарных тригонометрических уравнений.

Еще раз напомним: замену неизвестного следует делать при первой возможности, получившееся после замены уравнение необходимо решить до конца, включая этап отбора корней, а уж затем возвратится к первоначальному неизвестному.

Одна из особенностей тригонометрических уравнений заключается в том, что ответ во многих случаях может быть записан различными способами. Даже для решения уравнения ответ может быть записан следующим образом:

1) в виде двух серий: , ;

2) в стандартной форме представляющей собой объединение указанных выше серий: , ;

3) поскольку, то ответ можно записать в виде, . (В дальнейшем наличие параметра, или в записи ответа автоматически означает, что этот параметр принимает всевозможные целочисленные значения. Исключения будут оговариваться.)

Очевидно, что тремя перечисленными случаями не исчерпываются все возможности для записи ответа рассматриваемого уравнения (их бесконечно много).

Например, при справедливо равенство. Следовательно, в двух первых случаях, если, мы можем заменить на.

Обычно ответ записывается на основании пункта 2. Полезно запомнить следующую рекомендацию: если на решении уравнения работа не заканчивается, необходимо еще провести исследование, отбор корней, то наиболее удобна форма записи, указанная в пункте 1. (Аналогичную рекомендацию следует дать и для уравнения.)

Рассмотрим пример иллюстрирующий сказанное.

Пример Решить уравнение.

Решение. Наиболее очевидным является следующий путь. Данное уравнение распадается на два: и. Решая каждое из них и объединяя полученные ответы, найдем.

Другой путь. Поскольку, то, заменяя и по формулам понижения степени. После небольших преобразований получим, откуда.

На первый взгляд никаких особых преимуществ у второй формулы по сравнению с первой нет. Однако, если возьмем, например, то окажется, что, т.е. уравнение имеет решение, в то время как первый способ нас приводит к ответу. "Увидеть" и доказать равенство не так просто.

Тема: «Методы решения тригонометрических уравнений».

Цели урока:

образовательные:

Сформировать навыки различать виды тригонометрических уравнений;

Углубление понимания методов решения тригонометрических уравнений;

воспитательные:

Воспитание познавательного интереса к учебному процессу;

Формирование умения анализировать поставленную задачу;

развивающие:

Формировать навык проводить анализ ситуации с последующим выбором наиболее рационального выхода из нее.

Оборудование: плакат с основными тригонометрическими формулами, компьютер, проектор, экран.

Начнем урок с повторения основного приема решения любого уравнения: сведение его к стандартному виду. Путем преобразований линейные уравнения сводят к виду ах = в, квадратные – к виду ax 2 + bx + c =0. В случае тригонометрических уравнений необходимо свести их к простейшим, вида: sinx = a , cosx = a , tgx = a , которые легко можно решить.

В первую очередь, конечно, для этого необходимо использовать основные тригонометрические формулы, которые представлены на плакате: формулы сложения, формулы двойного угла, понижения кратности уравнения. Мы уже умеем решать такие уравнения. Повторим некоторые из них:

Вместе с тем существуют уравнения, решение которых требует знаний некоторых специальных приемов.

Темой нашего урока является рассмотрение этих приемов и систематизация методов решения тригонометрических уравнений.

Методы решения тригонометрических уравнений.

1. Преобразование к квадратному уравнению относительно какой-либо тригонометрической функции с последующей заменой переменной.

Рассмотрим каждый из перечисленных методов на примерах, но более подробно остановимся на двух последних, так как два первых мы уже использовали при решении уравнений.

1. Преобразование к квадратному уравнению относительно какой-либо тригонометрической функции.

2. Решение уравнений методом разложения на множители.

3. Решение однородных уравнений.

Однородными уравнениями первой и второй степени называются уравнения вида:

соответственно (а ≠ 0, b ≠ 0, с ≠ 0).

При решении однородных уравнений почленно делят обе части уравнения на cosx для (1) уравнения и на cos 2 x для (2). Такое деление возможно, так как sinx и cosx не равны нулю одновременно – они обращаются в нуль в разных точках. Рассмотрим примеры решения однородных уравнений первой и второй степени.

Запомним это уравнение: при рассмотрении следующего метода – введение вспомогательного аргумента, решим его другим способом.

4. Введение вспомогательного аргумента.

Рассмотрим уже решенное предыдущим методом уравнение:

Как видим, получается тот же результат.

Рассмотрим еще один пример:

В рассмотренных примерах было, в общем, понятно, на что требуется разделить исходное уравнение, чтобы ввести вспомогательный аргумент. Но может случиться, что не очевидно, какой делитель выбрать. Для этого существует специальная методика, которую мы сейчас и рассмотрим в общем виде. Пусть дано уравнение: