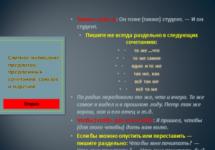
И т.п., логично познакомиться с уравнениями и других видов. Следующими по очереди идут линейные уравнения , целенаправленное изучение которых начинается на уроках алгебры в 7 классе.
Понятно, что сначала надо объяснить, что такое линейное уравнение, дать определение линейного уравнения, его коэффициентов, показать его общий вид. Дальше можно разбираться, сколько решений имеет линейное уравнение в зависимости от значений коэффициентов, и как находятся корни. Это позволит перейти к решению примеров, и тем самым закрепить изученную теорию. В этой статье мы это сделаем: детально остановимся на всех теоретических и практических моментах, касающихся линейных уравнений и их решения.
Сразу скажем, что здесь мы будем рассматривать только линейные уравнения с одной переменной, а уже в отдельной статье будем изучать принципы решения линейных уравнений с двумя переменными .
Навигация по странице.
Что такое линейное уравнение?
Определение линейного уравнения дается по виду его записи. Причем в разных учебниках математики и алгебры формулировки определений линейных уравнений имеют некоторые различия, не влияющие на суть вопроса.
Например, в учебнике алгебры для 7 класса Ю. Н. Макарычева и др. линейное уравнение определяется следующим образом:
Определение.
Уравнение вида a·x=b , где x – переменная, a и b – некоторые числа, называется линейным уравнением с одной переменной .
Приведем примеры линейных уравнений, отвечающие озвученному определению. Например, 5·x=10 – это линейное уравнение с одной переменной x , здесь коэффициент a равен 5 , а число b есть 10 . Другой пример: −2,3·y=0 – это тоже линейное уравнение, но с переменной y , в котором a=−2,3 и b=0 . А в линейных уравнениях x=−2 и −x=3,33 a не присутствуют в явном виде и равны 1 и −1 соответственно, при этом в первом уравнении b=−2 , а во втором - b=3,33 .
А годом ранее в учебнике математики Виленкина Н. Я. линейными уравнениями с одним неизвестным помимо уравнений вида a·x=b считали и уравнения, которые можно привести к такому виду с помощью переноса слагаемых из одной части уравнения в другую с противоположным знаком, а также с помощью приведения подобных слагаемых. Согласно этому определению, уравнения вида 5·x=2·x+6 , и т.п. тоже линейные.
В свою очередь в учебнике алгебры для 7 классов А. Г. Мордковича дается такое определение:
Определение.
Линейное уравнение с одной переменной x – это уравнение вида a·x+b=0 , где a и b – некоторые числа, называемые коэффициентами линейного уравнения.
К примеру, линейными уравнениями такого вида являются 2·x−12=0 , здесь коэффициент a равен 2 , а b – равен −12 , и 0,2·y+4,6=0 с коэффициентами a=0,2 и b=4,6 . Но в тоже время там приводятся примеры линейных уравнений, имеющие вид не a·x+b=0 , а a·x=b , например, 3·x=12 .
Давайте, чтобы у нас в дальнейшем не было разночтений, под линейным уравнениями с одной переменной x и коэффициентами a и b будем понимать уравнение вида a·x+b=0 . Такой вид линейного уравнения представляется наиболее оправданным, так как линейные уравнения – это алгебраические уравнения первой степени. А все остальные указанные выше уравнения, а также уравнения, которые с помощью равносильных преобразований приводятся к виду a·x+b=0 , будем называть уравнениями, сводящимися к линейным уравнениям . При таком подходе уравнение 2·x+6=0 – это линейное уравнение, а 2·x=−6 , 4+25·y=6+24·y , 4·(x+5)=12 и т.п. – это уравнения, сводящиеся к линейным.
Как решать линейные уравнения?
Теперь пришло время разобраться, как решаются линейные уравнения a·x+b=0 . Другими словами, пора узнать, имеет ли линейное уравнение корни, и если имеет, то сколько их и как их найти.
Наличие корней линейного уравнения зависит от значений коэффициентов a и b . При этом линейное уравнение a·x+b=0 имеет
- единственный корень при a≠0 ,
- не имеет корней при a=0 и b≠0 ,
- имеет бесконечно много корней при a=0 и b=0 , в этом случае любое число является корнем линейного уравнения.
Поясним, как были получены эти результаты.
Мы знаем, что для решения уравнений можно переходить от исходного уравнения к равносильным уравнениям , то есть, к уравнениям с теми же корнями или также как и исходное, не имеющим корней. Для этого можно использовать следующие равносильные преобразования:
- перенос слагаемого из одной части уравнения в другую с противоположным знаком,
- а также умножение или деление обе частей уравнения на одно и то же отличное от нуля число.
Итак, в линейном уравнении с одной переменной вида a·x+b=0 мы можем перенести слагаемое b из левой части в правую часть с противоположным знаком. При этом уравнение примет вид a·x=−b .
А дальше напрашивается деление обеих частей уравнения на число a. Но есть одно но: число a может быть равно нулю, в этом случае такое деление невозможно. Чтобы справиться с этой проблемой, сначала будем считать, что число a отлично от нуля, а случай равного нулю a рассмотрим отдельно чуть позже.
Итак, когда a не равно нулю, то мы можем обе части уравнения a·x=−b разделить на a , после этого оно преобразуется к виду x=(−b):a , этот результат можно записать с использованием дробной черты как .
Таким образом, при a≠0 линейное уравнение a·x+b=0 равносильно уравнению , откуда виден его корень .
Несложно показать, что этот корень единственный, то есть, линейное уравнение не имеет других корней. Это позволяет сделать метод от противного.
Обозначим корень как x 1 . Предположим, что существует еще один корень линейного уравнения, который обозначим x 2 , причем x 2 ≠x 1 , что в силу определения равных чисел через разность эквивалентно условию x 1 −x 2 ≠0 . Так как x 1 и x 2 корни линейного уравнения a·x+b=0 , то имеют место числовые равенства a·x 1 +b=0 и a·x 2 +b=0 . Мы можем выполнить вычитание соответствующих частей этих равенств, что нам позволяют сделать свойства числовых равенств , имеем a·x 1 +b−(a·x 2 +b)=0−0 , откуда a·(x 1 −x 2)+(b−b)=0 и дальше a·(x 1 −x 2)=0 . А это равенство невозможно, так как и a≠0 и x 1 −x 2 ≠0 . Так мы пришли к противоречию, что доказывает единственность корня линейного уравнения a·x+b=0 при a≠0 .
Так мы решили линейное уравнение a·x+b=0 при a≠0 . Первый результат, приведенный в начале этого пункта, обоснован. Остались еще два, отвечающие условию a=0 .
При a=0 линейное уравнение a·x+b=0 принимает вид 0·x+b=0 . Из этого уравнения и свойства умножения чисел на нуль следует, что какое бы число мы не взяли в качестве x , при его подстановке в уравнение 0·x+b=0 получится числовое равенство b=0 . Это равенство верное, когда b=0 , а в остальных случаях при b≠0 это равенство неверное.
Следовательно, при a=0 и b=0 любое число является корнем линейного уравнения a·x+b=0 , так как при этих условиях подстановка вместо x любого числа дает верное числовое равенство 0=0 . А при a=0 и b≠0 линейное уравнение a·x+b=0 не имеет корней, так как при этих условиях подстановка вместо x любого числа приводит к неверному числовому равенству b=0 .
Приведенные обоснования позволяют сформировать последовательность действий, позволяющую решить любое линейное уравнение. Итак, алгоритм решения линейного уравнения таков:
- Сначала по записи линейного уравнения находим значения коэффициентов a и b .
- Если a=0 и b=0 , то это уравнение имеет бесконечно много корней, а именно, любое число является корнем этого линейного уравнения.
- Если же a отлично от нуля, то
- коэффициент b переносится в правую часть с противоположным знаком, при этом линейное уравнение преобразуется к виду a·x=−b ,
- после чего обе части полученного уравнения делятся на отличное от нуля число a , что и дает искомый корень исходного линейного уравнения .
Записанный алгоритм является исчерпывающим ответом на вопрос, как решать линейные уравнения.
В заключение этого пункта стоит сказать, что похожий алгоритм применяется для решения уравнений вида a·x=b . Его отличие состоит в том, что при a≠0 сразу выполняется деление обеих частей уравнения на это число, здесь b уже находится в нужной части уравнения и не нужно осуществлять его перенос.
Для решения уравнений вида a·x=b применяется такой алгоритм:
- Если a=0 и b=0 , то уравнение имеет бесконечно много корней, которыми являются любые числа.
- Если a=0 и b≠0 , то исходное уравнение не имеет корней.
- Если же a отлично от нуля, то обе части уравнения делятся на отличное от нуля число a , откуда находится единственный корень уравнения, равный b/a .
Примеры решения линейных уравнений
Переходим к практике. Разберем, как применяется алгоритм решения линейных уравнений. Приведем решения характерных примеров, соответствующих различным значениям коэффициентов линейных уравнений.
Пример.
Решите линейное уравнение 0·x−0=0 .
Решение.
В этом линейном уравнении a=0 и b=−0 , что то же самое, b=0 . Следовательно, это уравнение имеет бесконечно много корней, любое число является корнем этого уравнения.
Ответ:
x – любое число.
Пример.
Имеет ли решения линейное уравнение 0·x+2,7=0 ?
Решение.
В данном случае коэффициент a равен нулю, а коэффициент b этого линейного уравнения равен 2,7 , то есть, отличен от нуля. Поэтому, линейное уравнение не имеет корней.
§ 23. Линейное уравнение с одной переменной. Решение линейных уравнений с одной переменной и уравнений, сводящихся к ним
Мы зна емо, как решать уравнения 2х = -8; х - 5; 0,01 х -17.
Каждое из этих уравнений имеет вид ах = b , где х - переменная, а и b - некоторые числа.
Числа а и b называют коэффициентами уравнения.
Если а ≠ 0, то уравнение ах = b называют уравнением первой степени с одной переменной. Поделив обе части уравнения на а, получим х = , то есть являетсяединственным корнем этого уравнения является число
Если а - 0 и b - 0, то линейное уравнение имеет вид 0х - 0. Корнем такого уравнения является любое число, так как при любом значении х значение левой и правой частей уравнения равны и равны нулю. Поэтому уравнение 0х = 0 множество корней.
Если а - 0, а b ≠ 0, то линейное уравнение примет вид 0х - b . При этом не существует никакого значения переменной х, которое бы превращало левую и правую части уравнения на одно и то же число. Ведь значение левой части уравнения при любом значении х равен нулю, а значение правой части - числу b , отличном от нуля. Поэтому уравнение 0х = b при b ≠ 0 не имеет корней.
Систематизируем данные о решения линейного уравнения ах = b в виде схемы:

Пример 1. Решить уравнение:
Р а з в ’ я з а н н я.
1) 0,2 х = 7; х = 7: 0,2; х = 35.
Ответ: - 4.
3)0х = 7; уравнение не имеет корней.
Ответ: корней не имеет.
Процесс решения многих уравнений является сводом этих уравнений к лилейным путем равносильных преобразований по свойствам уравнений.
Пример 2. Решить уравнение:
1) 3(х + 1) - 2х = 6 - 4х;
Р а з в ’ я з а н н я.
1. Избавимся от знаменателей (если они есть):
1)3(х + 3) - 2х = 6 - 4х.
Умножим обе частили уравнения на 6 (6 - наименьший общий знаменатель дробей). Имеем:
3(х + 1) + 2(5 - х) = х + 13.
2. Раскроем скобки (если они есть):
3х + 9 - 2х = 6 - 4х;
3х + 3 + 10 - 2х = х + 13.
3. Перенесем слагаемые, содержащие переменную, в левую часть, а остальные - в правую, изменив знаки этих слагаемых на противоположные:
3х - 2х + 4х = 6 - 9;
3х - 2х - х = 13 - 3 - 10.
4. Сведем подобные слагаемые:
5. Решим полученное линейное уравнение:
Ответ: -0,6.
х - любое число.
Ответ: любое число.
Пример 3. Решить уравнение 5(х + г) = 3х - 7р в отношении х.
Р а з в ’ я з а н н я. Раскроем скобки в левой части уравнения: 5х + 5р - 3х - 7р. Перенесем слагаемое 3х в левую часть, а 5р - в правую. Имеем: 5х - 3х = -7р - 5р; 2х = -12р. Тогда х = (-12р) : 2; х = (-12: 2)г; х = -6р.
Ответ: -6р.
Какое уравнение называют линейным уравнением с одной переменной? Приведите примеры линейных уравнений. В каком случае уравнение ах - b имеет единственный корень? В любом случае корнем уравнения ах - b -любое число? В каком случае уравнение ах = b не имеет корней?
848. (Устно) Какое из уравнений является линейным:
5) х + 7 = х 2 ;
849. (Устно) Сколько корней имеет уравнение:
850. Выясните, какое из данных уравнений имеет только одно решение, не имеет решений, имеет бесконечное множество решений:
851. (Устно) Решите уравнение:
2) 0,5 х = -2,5;
3) -2,5 х = 7,5;
852. Решите уравнение:
6) -0,01 х = 0,17;
8)-1,2 х = -4,2;
853. Найдите корень уравнения:
6) 0,1 х = 0,18.
854. Определите, что должно быть записано справа в уравнении вместо пробелов, если известно его корень:
855. Найдите корень уравнения:
1) 7х + 14 = 0;
2) 0, 3х - 21 = 0,5 х - 23;
3) 1х + 3 = 6х - 13;
4) 5х + (3х - 7) = 9;
5) 47 = 10 - (9х + 2);
6) (3х + 2) - (8х + 6) = 14.
856. Решите уравнение:
2) 1,4 х - 12 = 0,9 х + 4;
3) 3х + 14 = 5х - 16;
4) 12 - (5х + 10) = -3;
5) 6 - (8х + 11) = -1;
6) (3х - 4) - (6 - 4х) = 4.
857. Какое из уравнений равносильно уравнению 5х = 10:
3) х + 2 = х + 1;
5) х = 8 - 3х;
6)1х - 7 = 4х?
858. Являются ли уравнения равносильными:
1) 4х - х = 17 3х = 17;
2) 5х - 9 = 3х и 6х = 21;
3) 2х = -12 и х + 6 = 0;
4) 12х = 0 15х = 15?
859.
1) 3х + 7 равен -2;
2) 4(х + 1) равно значению выражения 5х - 9?
860. При каком значении у:
1) значение выражения 5у - 13 равна -3;
2) значения выражений 3(в - 2) и 13у - 8 равны между собой?
861. Решите уравнение:
2) 2х - у = 1;
862. Найдите корень уравнения:
863. Составьте линейное уравнение, корнем которого является:
1) число -2;
2) число -0,2.
864. Составьте линейное уравнение:
1) не имеет корней;
2) корнем которого является любое число.
865. Составьте линейное уравнение, корнем которого было бы:
1) число -8;
2) любое число.
866. Найдите корень уравнения:
1)(4х - 2) + (5х - 4) - 9 - (5 - 11х);
2) (7 - 8х) - (9 - 12х) - (5х + 4) = -16;
3) 3(4х - 5) - 10(2х - 1) = 33;
4) 9(3(х + 1) 2х) = 7(х + 1).
867. Решите уравнение:
1) (9х - 4) + (15х - 5) = 18 - (25 - 22х);
2) (10х + 6) - (9 - 9х) + (8 - 11х) = -19;
3) 7(х - 1) - 3(2х + 1) = -х - 15;
4) 5(4(х - 1) - 3х) = 9х.
868.
1) 2х + а = х + а;
2) b + х = с - х;
3) 6х + 2m = х - 8m ;
4) 9а + х = 3b - 2х.
Р а з в ’ я з а н н я.
4) 9a - х = 3b - 2х; х + 2х = 3b - 9а; 3х = 3(b - 3a). Поделим обе части уравнения на 3. Получим: х = b - 3а.
Ответ: b - 3а.
869. Решите уравнение относительно х:
1) 7х + m = 2х + m ;
2) а + х = 2m - х;
3) 3х + b = 9b - х;
4) 5р + 2х = 10 - 3х.
870. Являются ли равносильными уравнения:
1) 2х - 4 = 2 и 5(х - 3) + 1 = 3х - 8;
2) 5х + 3 = 8 и 7(х - 2) + 20 = 4х + 3;
3) 5х = 0 и 0 х = 5;
4) 7х + 1 = 7х 2 и 5(х + 1) = 5х + 5;
5) 0: х = 7 и 0 ∙ х = 7;
6) 3(х - 2) = 3х - 6 и 2(х + 7) - 2(х + 1) + 12?
871. При каком значении у значение выражения:
1) 5у + 7 в три раза больше значения выражения у + 5;
2) 2у - 4 на 7,4 больше значения выражения 3 - 7у?
872. При каком значении х значение выражения:
1) 7х + 8 вдвое больше значения выражения х + 7;
2) 5х - 8 па 17,2 меньше значения выражения х + 2 ?
873. Составьте уравнение, которое было бы равносильно уравнению 7(2х - 8) = 5(7х - 8) - 15х.
874. При каком значении а уравнение:
1) 2ах = 16 имеет корень, равный 4;
2) 3х имеет корень, равный ;
3) 5(а + 1)х = 40 имеет корень, равный -1 ?
875. При каком значении b корнем уравнения:
1) 3b х = -24 является число -4;
2) (2а - 5)х = 45 с число 3?
876. Решите уравнение:
1) 4х + 7 = 3(х - 2) + х:
2) 2х + 5 - 2(х - 4) + 13;
3) 2х(1 - 3х) + 5х(3 - х) = 17х - 8х 2 ;
4) (7х - 3 + 2х 2 - 4х - 5) - (6х 3 - х 2 + 2х) = 3х 2 - (6х - х 3).
877. Найдите корень уравнения:
1) 3(х - 2) + 4х = 7(х -1) + 1;
2) 2(х + 1) + х = 6(х + 3);
3) 3х(2 + х) - 4 (1 - х 2) = 7х 2 + 6х;
4) (х 2 + 4х - 8) - (7х - 2х 2 - 5) = 3х 2 - (3х + 3).
878. Решите уравнение.
§ 1 Что такое уравнение
Уравнением называют равенство, содержащее неизвестное, значение которого надо найти. Например, записи:
не являются уравнениями. Нет равенства, и значение переменной найти не требуется. Это просто буквенные выражения. А вот записи:
13х - 14 = 2х + 4
являются уравнениями.
Уравнения - это алгебраические модели реальных ситуаций. В процессе работы с моделью мы решаем уравнение.
Решить уравнение - значит найти все его корни или показать, что их нет. Корнем уравнения называют такое значение переменной, при котором уравнение обращается в верное числовое равенство. Для примера рассмотрим уравнение:
Если х = 4, то уравнение примет вид числового равенства:
2∙ 4 - 1 = 5 или 7 = 5
Это неверное числовое равенство, а значит число 4 не является корнем уравнения. Если же х = 3, то уравнение примет вид числового равенства:
2∙ 3 - 1 = 5 или 5 = 5
Это верное числовое равенство, а значит число 3 является корнем уравнения. Причём других корней нет.
§ 2 Линейные уравнения с одной переменной
Уравнение вида ах + b = 0 называют линейным уравнением с одной переменной.
Здесь а и b - коэффициенты, они могут быть выражены любыми числами.
Давайте рассмотрим различные случаи.
1) Если а = 0 и b = 0, то уравнение примет вид 0 ∙ х + 0 = 0. Очевидно, что это уравнение имеет бесконечно много корней, так как любое число при умножении на ноль даёт 0. А значит в результате всегда будет верное числовое равенство.
2) Если а = 0, b ≠0. Тогда уравнение примет вид 0 ∙ х + b = 0. Можно заметить, что такое уравнение не будет иметь ни одного корня. В самом деле, при умножении любого числа на 0 в результате всегда будет получаться 0, но в сумме с числом, отличным от нуля, будет результат отличный от нуля, а значит в любом случае получится неверное числовое равенство.
3) Коэффициент а отличен от нуля, это самый распространенный случай. Рассуждаем так:
Сначала перенесём известное слагаемое в b правую часть уравнения, поменяв знак. Получим:
Затем разделим обе части уравнения на число а. Получим:
Значит в этом случае уравнение имеет только один корень, а именно:
Подведя итоги вышесказанному, можно сделать вывод:
Линейные уравнения с одним неизвестным могут иметь один корень, бесконечно много корней или не иметь ни одного корня.
А как быть, если уравнение записано в более сложном виде? Например, в виде:
4(х - 4) = 2х + 6
В этом случае нам придётся сначала провести ряд преобразований.
Сначала раскроем скобки. Получим:
4х - 16 = 2х + 6
Затем перенесём неизвестные слагаемые в левую часть уравнения, а известные в правую, не забыв поменять знак слагаемого при переносе. Получим:
4х - 2х = 6 + 16
Теперь приведём подобные слагаемые. Получим:
Поделив обе части уравнения на 2 имеем х = 11.
§ 3 Примеры использования понятия «линейное уравнение»
Рассмотрим ещё несколько примеров с использованием понятия «линейное уравнение».
Пример 1. Определить количество корней уравнения 3х + 15 = 3(х +2) + 9.
Это линейное уравнение с одной переменной. Чтобы ответить на вопрос надо сначала преобразовать данное уравнение. Для этого раскроем скобки, получим:
3х + 15 = 3х + 6 + 9
Перенесём известные слагаемые в правую часть уравнения, а неизвестные в левую. Получим:
3х - 3х = 6 + 9 - 15
Приведём подобные слагаемые, получим:
Это равенство верно при любых значениях х, поэтому уравнение имеет бесконечно много корней.
Пример 2. При каком значении переменной значение выражения 4у - 1 равно значению выражения 3у + 5?
Здесь явно задаётся условие равенства двух выражений. Запишем это равенство, получим:
4у - 1 = 3у + 5
Решив это уравнение способом из примера 1 получим у = 6.
Ответ: значения выражений равны при у = 6.
Пример 3. Маме и дочке вместе 35 лет. Сколько лет дочке, если она на 25 лет моложе мамы?
Составим алгебраическую модель данной реальной ситуации. Пусть дочке х лет, тогда маме х + 25 лет. Так как по условию вместе им 35 лет, то составим уравнение:
х + (х + 25) = 35
Решая это уравнение, находим:
Так как буквой х мы обозначили возраст дочки, то найденное число является ответом на вопрос задачи. Ответ: дочке 5 лет.
Список использованной литературы:
- Мордкович А.Г, Алгебра 7 класс в 2 частях, Часть 1, Учебник для общеобразовательных учреждений/ А.Г. Мордкович. – 10 – е изд., переработанное – Москва, «Мнемозина», 2007
- Мордкович А.Г., Алгебра 7 класс в 2 частях, Часть 2, Задачник для общеобразовательных учреждений/ [А.Г. Мордкович и др.]; под редакцией А.Г. Мордковича – 10-е издание, переработанное – Москва, «Мнемозина», 2007
- Е.Е. Тульчинская, Алгебра 7 класс. Блиц опрос: пособие для учащихся общеобразовательных учреждений, 4-е издание, исправленное и дополненное, Москва, «Мнемозина», 2008
- Александрова Л.А., Алгебра 7 класс. Тематические проверочные работы в новой форме для учащихся общеобразовательных учреждений, под редакцией А.Г. Мордковича, Москва, «Мнемозина», 2011
- Александрова Л.А. Алгебра 7 класс. Самостоятельные работы для учащихся общеобразовательных учреждений, под редакцией А.Г. Мордковича – 6-е издание, стереотипное, Москва, «Мнемозина», 2010
Тема урока:
Линейное уравнение с одной переменной
Куделько Марины
Цели урока:
Образовательные: закрепить понятие уравнения, корни уравнения, вспомнить, что означает решить уравнение, ввести и усвоить понятие равносильного уравнения, линейного уравнения, уметь находить линейные уравнения и научиться решать их, ученики должны знать, сколько корней может иметь линейное уравнение.
Развивающие: Развивать у учащихся аккуратность оформления записей, вычислительные навыки учащихся, формировать интерес и любовь к предмету, память и мыслительные операции, формировать умения четко и ясно излагать свои мысли, четко формировать вопросы.
Воспитательные: Способствовать выявлению и раскрытию способностей учащихся, прививать самостоятельность.
Тип урока: изучение нового материала.
План урока:
.Проверка домашнего задания (5 минут)
Так как сегодняшний урок-это урок изучения нового материала, времени на проверку домашнего задания нет, я соберу тетради на проверку, заранее предупредив учеников. Тетради ученики положат на край парты.
.Актуализация опорных знаний
В начале урока нужно вместе с учениками вспомнить уже знакомые понятия уравнения, корня уравнения, вспомнить смысл требования решить уравнение. Учитель проводит фронтальный опрос. А также учитель заранее приготовил на доске маленькие примеры по данным вопросы, ученики выходят к доске и самостоятельно решают, желательно без помощи учителя, так как уже это пройденный материал.
Доказать, что каждое из чисел -5, 0 ,3 является корнем уравнения:
А) z(z-3)(z+5)=0;
Решить уравнение:
Найдите корень уравнения:
Так как в данной теме нам нужно работать с понятием, неизвестным для учеников, то мы его должны сначала ввести. Это понятие - равносильные уравнения. Можно сначала дать несколько уравнений, попросить, чтобы ученики решили их. Потом спросить, что между уравнениями общего. Окажется, что общее между уравнениями - это их одинаковые корни. Если ученики сразу не поймут, то нужно дать еще парочку примеров. И сказать, что такого типа уравнения называются равносильными. Т.е. равносильные уравнения - это уравнения, имеющие одни и те же корни.
Являются ли уравнения равносильными???
Можно привести таблички на доске (или на интерактивной доске):
3. Изучение нового материала
Теперь, когда нужные понятия были вспомнены, некоторые понятия успешно введены, преступим к изучению нового материала.
Учитель заранее подготовил на доске рисунке (или презентацию на эту тему, что намного лучше).
Учитель предлагает задачу ученикам.
Решим уравнение, которое можно наглядно представить на рисунках: корень линейный равносильный уравнение
Мы представили условие уравнения в виде рисунка, что намного нагляднее и понятнее ученикам. Нам даны весы, на которых стоят чашки чая и гирьки, и взаимно друг друга уравновешивают.
Теперь мы будем рассуждать, что будет происходить с нашими весами, если мы отнимем или прибавим одинаковое количество пачек чая.
Рассуждать можно так. Равновесие часов не нарушится, если с каждой чашки снять по 3 пачки чая. (Это видно на рисунке 2).Если 2 пачки чая (!!одинакового веса!!) весят 150г., то одна пачка чая весит 150г. : 2 = 75г.
Эти рассуждения показывают такой путь решения данного уравнения. Вычтем из левой и правой частей уравнения выражение. Получим:
Слагаемые и - в правой части дают нуль. Поэтому получаем:
Значит, ответ.Эти действия учитель делает вместе с учениками, они ему должны подсказывать и помогать. Учитель может попросить повторить сказанное или, что лучше, объяснить эту задачу друг другу в парах, а один или пара учеников потом у доски. Учитель не забывает про похвалу учащихся.
Потом вместе, фронтально, решаем следующий пример.
Решим уравнение:
Если к каждой части уравнения прибавить выражение, то после привидения подобных в правой части не будет слагаемых с переменной, сделаем это (учитель просит проговаривать учеников вслух действия, может спросить у отдельного ученика проговорить или объяснить):
(Приведем подобные и заметим, что 3x и -3x взаимно уничтожатся.)
Сравнивая полученное уравнение с данным, замечаем, что слагаемое - перешло из правой части в левую с противоположным знаком. Приводим подобные в левой части:
Замечаем, что уравнение получается из уравнения после переноса числа из левой части уравнения в правую с противоположным знаком.
Находим, наконец, :
Замечаем, что если в уравнении любое слагаемое перенести из одной части в другую, изменив его знак, то получится уравнение, равносильное данному.
Переносят слагаемое не просто так, а чтобы в левой части были слагаемые с переменной, а в другой - известные числа. В левой части - неизвестные, в правой - известные.
Если уравнение содержит скобки, то сначала их нужно раскрыть.
Репетиторство
Нужна помощь по изучению какой-либы темы?
Наши специалисты проконсультируют или окажут репетиторские услуги по интересующей вас тематике.
Отправь заявку
с указанием темы прямо сейчас, чтобы узнать о возможности получения консультации.
В этом видео мы разберём целый комплект линейных уравнений, которые решаются по одному и тому же алгоритму — потому и они и называются простейшими.
Для начала определимся: что такое линейное уравнение и какое их них называть простейшим?
Линейное уравнение — такое, в котором присутствует лишь одна переменная, причём исключительно в первой степени.
Под простейшим уравнением подразумевается конструкция:
Все остальные линейные уравнения сводятся к простейшим с помощью алгоритма:
- Раскрыть скобки, если они есть;
- Перенести слагаемые, содержащие переменную, в одну сторону от знака равенства, а слагаемые без переменной — в другую;
- Привести подобные слагаемые слева и справа от знака равенства;
- Разделить полученное уравнение на коэффициент при переменной $x$ .
Разумеется, этот алгоритм помогает не всегда. Дело в том, что иногда после всех этих махинаций коэффициент при переменной $x$ оказывается равен нулю. В этом случае возможны два варианта:
- Уравнение вообще не имеет решений. Например, когда получается что-нибудь в духе $0\cdot x=8$, т.е. слева стоит ноль, а справа — число, отличное от нуля. В видео ниже мы рассмотрим сразу несколько причин, по которым возможна такая ситуация.
- Решение — все числа. Единственный случай, когда такое возможно — уравнение свелось к конструкции $0\cdot x=0$. Вполне логично, что какой бы $x$ мы ни подставили, все равно получится «ноль равен нулю», т.е. верное числовое равенство.
А теперь давайте посмотрим, как всё это работает на примере реальных задач.
Примеры решения уравнений
Сегодня мы занимаемся линейными уравнениями, причем только простейшими. Вообще, под линейным уравнением подразумевается всякое равенство, содержащее в себе ровно одну переменную, и она идет лишь в первой степени.
Решаются такие конструкции примерно одинаково:
- Прежде всего необходимо раскрыть скобки, если они есть (как в нашем последнем примере);
- Затем свести подобные
- Наконец, уединить переменную, т.е. всё, что связано с переменной — слагаемые, в которых она содержится — перенести в одну сторону, а всё, что останется без неё, перенести в другую сторону.
Затем, как правило, нужно привести подобные с каждой стороны полученного равенства, а после этого останется лишь разделить на коэффициент при «иксе», и мы получим окончательный ответ.
В теории это выглядит красиво и просто, однако на практике даже опытные ученики старших классов могут допускать обидные ошибки в достаточно простых линейных уравнениях. Обычно ошибки допускаются либо при раскрытии скобок, либо при подсчёте «плюсов» и «минусов».
Кроме того, бывает так, что линейное уравнение вообще не имеет решений, или так, что решением является вся числовая прямая, т.е. любое число. Эти тонкости мы и разберем в сегодняшнем уроке. Но начнем мы, как вы уже поняли, с самых простых задач.
Схема решения простейших линейных уравнений
Для начала давайте я еще раз напишу всю схему решения простейших линейных уравнений:
- Раскрываем скобки, если они есть.
- Уединяем переменные, т.е. все, что содержит «иксы» переносим в одну сторону, а без «иксов» — в другую.
- Приводим подобные слагаемые.
- Разделяем все на коэффициент при «иксе».
Разумеется, эта схема работает не всегда, в ней есть определенные тонкости и хитрости, и сейчас мы с ними и познакомимся.
Решаем реальные примеры простых линейных уравнений
Задача №1
На первом шаге от нас требуется раскрыть скобки. Но их в этом примере нет, поэтому пропускаем данный этап. На втором шаге нам нужно уединить переменные. Обратите внимание: речь идет лишь об отдельных слагаемых. Давайте запишем:
Приводим подобные слагаемые слева и справа, но тут уже это сделано. Поэтому переходим к четвертому шагу: разделить на коэффициент:
\[\frac{6x}{6}=-\frac{72}{6}\]
Вот мы и получили ответ.
Задача №2
В этой задаче мы можем наблюдать скобки, поэтому давайте раскроем их:
И слева и справа мы видим примерно одну и ту же конструкцию, но давайте действовать по алгоритму, т.е. уединяем переменные:
Приведем подобные:
При каких корнях это выполняется. Ответ: при любых. Следовательно, можно записать, что $x$ — любое число.
Задача №3
Третье линейное уравнение уже интересней:
\[\left(6-x \right)+\left(12+x \right)-\left(3-2x \right)=15\]
Тут есть несколько скобок, однако они ни на что не умножаются, просто перед ними стоят различные знаки. Давайте раскроем их:
Выполняем второй уже известный нам шаг:
\[-x+x+2x=15-6-12+3\]
Посчитаем:
Выполняем последний шаг — делим все на коэффициент при «икс»:
\[\frac{2x}{x}=\frac{0}{2}\]
Что необходимо помнить при решении линейных уравнений
Если отвлечься от слишком простых задач, то я бы хотел сказать следующее:
- Как я говорил выше, далеко не каждое линейное уравнение имеет решение — иногда корней просто нет;
- Даже если корни есть, среди них может затесаться ноль — ничего страшного в этом нет.
Ноль — такое же число, как и остальные, не стоит его как-то дискриминировать или считать, что если у вас получился ноль, то вы что-то сделали неправильно.
Еще одна особенность связана с раскрытием скобок. Обратите внимание: когда перед ними стоит «минус», то мы его убираем, однако в скобках знаки меняем на противоположные . А дальше мы можем раскрывать ее по стандартным алгоритмам: мы получим то, что видели в выкладках выше.
Понимание этого простого факта позволит вам не допускать глупые и обидные ошибки в старших классах, когда выполнение подобных действий считается самим собой разумеющимся.
Решение сложных линейных уравнений
Перейдем к более сложным уравнениям. Теперь конструкции станут сложнее и при выполнении различных преобразований возникнет квадратичная функция. Однако не стоит этого бояться, потому что если по замыслу автора мы решаем линейное уравнение, то в процессе преобразования все одночлены, содержащие квадратичную функцию, обязательно сократятся.
Пример №1
Очевидно, что первым делом нужно раскрыть скобки. Давайте это сделаем очень аккуратно:
Теперь займемся уединением:
\[-x+6{{x}^{2}}-6{{x}^{2}}+x=-12\]
Приводим подобные:
Очевидно, что у данного уравнения решений нет, поэтому в ответе так и запишем:
\[\varnothing \]
или корней нет.
Пример №2
Выполняем те же действия. Первый шаг:
Перенесем все, что с переменной, влево, а без нее — вправо:
Приводим подобные:
Очевидно, что данное линейное уравнение не имеет решения, поэтому так и запишем:
\[\varnothing \],
либо корней нет.
Нюансы решения
Оба уравнения полностью решены. На примере этих двух выражений мы ещё раз убедились, что даже в самых простых линейных уравнениях всё может быть не так просто: корней может быть либо один, либо ни одного, либо бесконечно много. В нашем случае мы рассмотрели два уравнения, в обоих корней просто нет.
Но я бы хотел обратить ваше внимание на другой факт: как работать со скобками и как их раскрывать, если перед ними стоит знак «минус». Рассмотрим вот это выражение:
Прежде чем раскрывать, нужно перемножить всё на «икс». Обратите внимание: умножается каждое отдельное слагаемое . Внутри стоит два слагаемых — соответственно, два слагаемых и умножается.
И только после того, когда эти, казалось бы, элементарные, но очень важные и опасные преобразования выполнены, можно раскрывать скобку с точки зрения того, что после неё стоит знак «минус». Да, да: только сейчас, когда преобразования выполнены, мы вспоминаем, что перед скобками стоит знак «минус», а это значит, что все, что в низ, просто меняет знаки. При этом сами скобки исчезают и, что самое главное, передний «минус» тоже исчезает.
Точно также мы поступаем и со вторым уравнением:
Я не случайно обращаю внимание на эти мелкие, казалось бы, незначительные факты. Потому что решение уравнений — это всегда последовательность элементарных преобразований, где неумение чётко и грамотно выполнять простые действия приводит к тому, что ученики старших классов приходят ко мне и вновь учатся решать вот такие простейшие уравнения.
Разумеется, придёт день, и вы отточите эти навыки до автоматизма. Вам уже не придётся каждый раз выполнять столько преобразований, вы всё будете писать в одну строчку. Но пока вы только учитесь, нужно писать каждое действие отдельно.
Решение ещё более сложных линейных уравнений
То, что мы сейчас будем решать, уже сложно назвать простейшими задача, однако смысл остается тем же самым.
Задача №1
\[\left(7x+1 \right)\left(3x-1 \right)-21{{x}^{2}}=3\]
Давайте перемножим все элементы в первой части:
Давайте выполним уединение:
Приводим подобные:
Выполняем последний шаг:
\[\frac{-4x}{4}=\frac{4}{-4}\]
Вот наш окончательный ответ. И, несмотря на то, что у нас в процессе решения возникали коэффициенты с квадратичной функцией, однако они взаимно уничтожились, что делает уравнение именно линейным, а не квадратным.
Задача №2
\[\left(1-4x \right)\left(1-3x \right)=6x\left(2x-1 \right)\]
Давайте аккуратно выполним первый шаг: умножаем каждый элемент из первой скобки на каждый элемент из второй. Всего должно получиться четыре новых слагаемых после преобразований:
А теперь аккуратно выполним умножение в каждом слагаемом:
Перенесем слагаемые с «иксом» влево, а без — вправо:
\[-3x-4x+12{{x}^{2}}-12{{x}^{2}}+6x=-1\]
Приводим подобные слагаемые:
Мы вновь получили окончательный ответ.
Нюансы решения
Важнейшее замечание по поводу этих двух уравнений состоит в следующем: как только мы начинаем умножать скобки, в которых находится более чем оно слагаемое, то выполняется это по следующему правилу: мы берем первое слагаемое из первой и перемножаем с каждым элементом со второй; затем берем второй элемент из первой и аналогично перемножаем с каждым элементом со второй. В итоге у нас получится четыре слагаемых.
Об алгебраической сумме
На последнем примере я хотел бы напомнить ученикам, что такое алгебраическая сумма. В классической математике под $1-7$ мы подразумеваем простую конструкцию: из единицы вычитаем семь. В алгебре же мы подразумеваем под этим следующее: к числу «единица» мы прибавляем другое число, а именно «минус семь». Этим алгебраическая сумма отличается от обычной арифметической.
Как только при выполнении всех преобразований, каждого сложения и умножения вы начнёте видеть конструкции, аналогичные вышеописанным, никаких проблем в алгебре при работе с многочленами и уравнениями у вас просто не будет.
В заключение давайте рассмотрим ещё пару примеров, которые будут ещё более сложными, чем те, которые мы только что рассмотрели, и для их решения нам придётся несколько расширить наш стандартный алгоритм.
Решение уравнений с дробью
Для решения подобных заданий к нашему алгоритму придется добавить еще один шаг. Но для начала я напомню наш алгоритм:
- Раскрыть скобки.
- Уединить переменные.
- Привести подобные.
- Разделить на коэффициент.
Увы, этот прекрасный алгоритм при всей его эффективности оказывается не вполне уместным, когда перед нами дроби. А в том, что мы увидим ниже, у нас и слева, и справа в обоих уравнениях есть дробь.
Как работать в этом случае? Да всё очень просто! Для этого в алгоритм нужно добавить ещё один шаг, который можно совершить как перед первым действием, так и после него, а именно избавиться от дробей. Таким образом, алгоритм будет следующим:
- Избавиться от дробей.
- Раскрыть скобки.
- Уединить переменные.
- Привести подобные.
- Разделить на коэффициент.
Что значит «избавиться от дробей»? И почему выполнять это можно как после, так и перед первым стандартным шагом? На самом деле в нашем случае все дроби являются числовыми по знаменателю, т.е. везде в знаменателе стоит просто число. Следовательно, если мы обе части уравнения домножим на это число, то мы избавимся от дробей.
Пример №1
\[\frac{\left(2x+1 \right)\left(2x-3 \right)}{4}={{x}^{2}}-1\]
Давайте избавимся от дробей в этом уравнении:
\[\frac{\left(2x+1 \right)\left(2x-3 \right)\cdot 4}{4}=\left({{x}^{2}}-1 \right)\cdot 4\]
Обратите внимание: на «четыре» умножается все один раз, т.е. если у вас две скобки, это не значит, что каждую из них нужно умножать на «четыре». Запишем:
\[\left(2x+1 \right)\left(2x-3 \right)=\left({{x}^{2}}-1 \right)\cdot 4\]
Теперь раскроем:
Выполняем уединение переменной:
Выполняем приведение подобных слагаемых:
\[-4x=-1\left| :\left(-4 \right) \right.\]
\[\frac{-4x}{-4}=\frac{-1}{-4}\]
Мы получили окончательное решение, переходим ко второму уравнению.
Пример №2
\[\frac{\left(1-x \right)\left(1+5x \right)}{5}+{{x}^{2}}=1\]
Здесь выполняем все те же действия:
\[\frac{\left(1-x \right)\left(1+5x \right)\cdot 5}{5}+{{x}^{2}}\cdot 5=5\]
\[\frac{4x}{4}=\frac{4}{4}\]
Задача решена.
Вот, собственно, и всё, что я хотел сегодня рассказать.
Ключевые моменты
Ключевые выводы следующие:
- Знать алгоритм решения линейных уравнений.
- Умение раскрывать скобки.
- Не стоит переживать, если где-то у вас появляются квадратичные функции, скорее всего, в процессе дальнейших преобразований они сократятся.
- Корни в линейных уравнениях, даже самых простых, бывают трех типов: один единственный корень, вся числовая прямая является корнем, корней нет вообще.
Надеюсь, этот урок поможет вам освоить несложную, но очень важную для дальнейшего понимания всей математики тему. Если что-то непонятно, заходите на сайт, решайте примеры, представленные там. Оставайтесь с нами, вас ждет еще много интересного!